Квадратный корень

Раздел долгосрочного плана:

Квадратные корни и иррациональные выражения

8.1.1.2

знать определения и различать понятия квадратного корня и арифметического квадратного корня;

• объснить различие между понятиями «квадратный корень» и «арифметический квадратный корень»;
• извлекать арифметический квадратный корень из точного квадрата;
• решать уравнения вида , где .

Критерии оценивания

• знает определения понятий квадратного корня и арифметического квадратного корня;
• объясняет различие между квадратным корнем и арифметическим квадратным корнем;
• извлекать арифметический квадратный корень из точного квадрата;
• решает уравнения вида , где .

Учащиеся могут:

Вести рассуждения о квадратном корне и арифметическом квадратном корне из числа.

Лексика и терминология, специфичная для предмета:

квадратный корень, арифметический квадратный корень, корень из точного квадрата, радикал, иррациональное выражение, подкоренное выражение

Полезные выражения для диалогов и письма:

Вычислим квадратный корень из числа 25, квадратный корень из числа -25 не существует, потому что …

Квадратным корнем из неотрицательного числа a называют…

Арифметическим квадратным корнем из неотрицательного числа a называют…

Квадратный корень и арифметический квадратный корень отличаются тем, что …

Межпредметные связи

Учащиеся в 7 классе изучили раздел «Степень с целым показателем». Перед изучением темы осуществляется повторение понятия степени числа, в частности, возведение числа в квадрат, через устный опрос и выполнение заданий. Также в ходе устного опроса будет повторяться понятия действительного числа и иррационального числа.

Учащиеся также знают таблицу квадратов чисел от 0 до 30.

Начало урока

0-2 мин

2-5 мин

5-8 мин

8-11 мин

1. Организационный момент.

В начале урока сделать акцент на концентрацию внимания учащихся.

1. Повторение.

Учитель посредством беседы с учащимися напоминает им ключевые понятия, которые будут необходимы при изучении нового материала: иррациональное число, степени рациональных чисел, в частности, возведение рационального числа в квадрат. Затем учащимся предлагается индивидуально выполнить задание, направленное на закрепление навыков возведения в квадрат рациональных чисел, после выполнения которого учащимися проводится самопроверка по презентации.

1. Стадия вызова.

Учитель напоминает учащимся, что если у числа имеется показатель второй степени, то число умножается на себя 2 раза (в квадрате). В следствие этого, если мы хотим найти обратную величину полученного значения, мы извлекаем квадратный корень. Забегая вперед, учитель показывает учащимся новый для них математический символ «».

Аналогично если число возвести в 3 степень (в куб), чтобы найти обратную величину, мы извлекаем кубический корень. Далее демонстрируется математический символ «».

Также есть корень, который будет обратной величиной каждого показателя степени. Далее демонстрируется математический символ «».

1. Целеполагание.

Учитель объявляет тему урока и цели обучения. Совместно с учащимися формулируются цели урока. Далее учитель озвучивает критерии оценивания, определяет «зону ближайшего развития» учащихся, ожидания к концу урока.

Презентация

Слайд 1

Мел, доска

Презентация

Слайды 2-4

Середина урока

11-16 мин

16-17 мин

17-22 мин

22-25 мин

25-29 мин

29-32 мин

32-38 мин

1. Объяснение нового материала и его первичное закрепление.

Учителем делается прежде всего акцент на том, что операция извлечения квадратного корня из числа обратна операции возведения числа в квадрат. Далее вводится определение понятия квадратного корня и его обозначение, рассматривается понятие подкоренного выражения.

Посредством анализа определения квадратного корня, учащимися совместно с учителем устанавливается условие, накладываемое на подкоренное выражение. Затем учитель объясняет в каком случае выражение не имеет смысл. Учащимся учитель предлагает объяснить почему это так.

Немного из истории математики.

Далее учащимся дается небольшая информация об истории введения математического знака радикала «».

Решение задачи. Площадь квадрата равна 144 см кв. Чему равна длина стороны этого квадрата?

С помощью решения данной задачи учитель наталкивает учащихся на понятие арифметического квадратного корня, при этом учитель демонстрирует доказательство того, что число 12 является арифметическим квадратным корнем числа 144.

В ходе решения задачи учащимся задается вопрос: Чем отличаются квадратный корень и арифметический квадратный корень? Затем учитель предлагает учащимся самостоятельно сформулировать определение арифметического квадратного корня. После ответов учащихся, учитель формулирует точное определение. При этом учитель отмечает, что запись читают: «квадратный корень из a» (слово «арифметический» при этом опускают).

После решения задачи учитель предлагает учащимся прокомментировать рисунки, приведенные на слайде.

Упражнения для закрепления изученного.

I. Учитель предлагает учащимся индивидуально выполнить задания на извлечение квадратных корней из точных квадратов, в задании имеются также и выражения, не имеющие смысла, которые учащимся необходимо распознать и сделать запись, объясняющую почему это так. После выполнения задания учащимися выполняется самопроверка по готовым ответам, представленным на слайде. Затем учитель предлагает отдельным учащимся объяснить почему некоторые выражения не имеют смысла.

Критерии оценивания:

• Верно извлекает арифметический квадратный корень из точного квадрата;
• Верно определяет выражения, не имеющие смысла;
• Объясняет почему эти выражения не имеют смысла.

Учитель дает обратную связь на выполненное задание, акцентируя внимание учащихся на условие, при котором выражение имеет смысл.

В качестве замечания учитель отмечает, что корни квадратные из точного квадрата является рациональным числом, в противном случае, оно будет иррациональным, как например, числа и т.д.

II. Далее учитель предлагает учащимся обсуждая в парах, выполнить следующие задания на доказательство:

1) Число 5 — арифметический квадратный корень из 25;

2) Число 0,4 – арифметический квадратный корень из 0,16;

3) Число (– 8) не является арифметическим квадратным корнем из 64;

4) Число 0,6 не является арифметическим квадратным корнем из 3,6.

После выполнения задания учащимися выполняется самопроверка в парах по готовым ответам, представленным на слайде.

Критерии оценивания:

• Верно применяет определение арифметического квадратного корня;
• Верно доказывает предложенные утверждения.

При необходимости учитель комментирует доказательства утверждений.

Вывод основного свойства арифметического квадратного корня.

Учитель предлагает учащимся индивидуально выполнить задания на вычисление: , , . После выполнения первых двух примеров, учитель задает учащимся вопрос «Что вы заметили?». Затем предлагается записать установленную закономерность в виде формулы и применить эту формулу для выполнения третьего примера. После учащиеся отвечают на вопрос «В каком случае справедливо это свойство?» и обоснывают свой ответ.

Изучение основного свойства арифметического квадратного корня сопровождается поэтапными комментариями, представленными на слайде. В итоге учащиеся должны прийти к формуле: и к тому, что из определения арифметического квадратного корня следует, что если выражение имеет смысл, то и .

Критерии оценивания:

• Верно извлекает арифметический квадратный корень из точного квадрата;
• Верно записывает основное свойство арифметического квадратного корня в виде формулы;
• Обосновывают основное свойство арифметического квадратного корня с помощью определения арифметического квадратного корня.

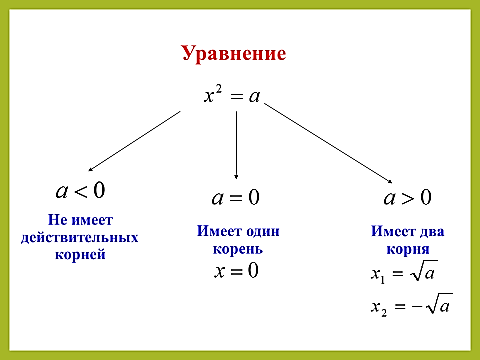
Решение уравнений вида , где .

Учащимся предлагается выполнить работу в группах из 3-4 учащихся: проанализировать решение предложенного уравнения, затем решить еще два уравнения. Затем сделать вывод по всем представленным случаям. А также объяснить какой смысл имеют равенства и на множестве действительных чисел.

Критерии оценивания:

• Верно решает уравнения вида , где ;
• Делает вывод о количестве решений уравнений вида , в зависимости от значения ;
• Объясняет различие между равенствами и , основываясь на различие между понятиями «квадратный корень» и «арифметический квадратный корень».

После выполнения заданий и проверки работы учащихся, учитель подводит итоги с помощью следующей схемы:

Затем учитель обращает внимание учащихся на то, что , а если , то х=-3 или х=3.

Презентация

Слайд 5

Презентация

Слайд 6

Презентация

Слайды 7-8

Презентация

Слайд 9

Приложение 1

Презентация

Слайд 10

Приложение 2

Презентация

Слайд 11

Презентация

Слайд 12

Приложение 3

Презентация

Слайд 13

Презентация

Слайд 14

Конец урока

38-40 мин

1. Подведение итогов урока.

Учитель возвращается к целям урока, обсуждая уровень их достижения. Для дальнейшего планирования уроков учащимся задаются вопросы:

— что узнал, чему научился;

— что осталось непонятным;

— над чем необходимо работать.

Вопросы могут обсуждаться устно или письменно.

В качестве домашнего задания учащимся можно предложить дополнительные разноуровневые задания, приведенные в методических рекомендациях.

Презентация

Слайд 15

Стикеры

Методические рекомендации к проведению урока

Здоровье и соблюдение техники безопасности

Урок будет построен таким образом, что ученики, которые не столь уверены в своих силах будут работать в парах, в которых работая с более способными учениками они смогут узнать больше. Способные же учащиеся могут проявить свои способности в качестве консультанта.

Во время работы в парах или индивидуально Вы можете помогать неуверенным ученикам, задавая наводящие вопросы.

Формативное оценивание производится на каждом этапе урока (самооценивание, оценивание учителем по критериям). Оценка путем наблюдения за вовлечением учеников при выполнении заданий и за участием в диалогах.

Прогресс, ответная реакция на задания в парах, в группах будут тщательно рассмотрены для того, чтобы оценить вклад каждого ученика и выявить наличие ошибок для их коррекции.