Пифагор теоремасы туралы бірер сөз
Теореманың тарихы
Теоременың тарихы ежелгі Қытайдан бастау алады. Ондағы негізгі назар аудартатын математикалық кітап Чу – пей. Бұл шығармада қабырғалары 3,4,5 – ке тең пифагор үшбұрышы туралы айтылады.
Егер тік бұрышты құрайтын 3 – ке тең қабырға мен 4 – ке тең биіктіктің ұштарын қоссақ пайда болған түзу 5 – ке тең болады..
Кантор (ұлы неміс математика тарихын зерттеуші) бұл кітапта үнді Бхаскар геометриясындағы сызбанұсқаға ұқсас сурет бар, деп есептеген.
Бұл теңдік египтіктерге б .з.д. 2300 жылы Аменемхета I патшаның кезінде белгілі болған (Берлин музейіндегі 6619 — жазбалар бойынша).
Кантордың ойынша гарпедонаптар немесе «арқан тартушылар» тік бұрышты қабырғалары 3,4,5 – ке тең тікбұрышты үшбұрыштар арқылы тұрғызған. Олардың құрылу әдісін оңай көрсетуге болады. Ұзындығы 12 метрге тең арқанды алып,бір ұшынан 3 метр,екінші ұшынан 4 метр арақашықтықты өлшеп белгілейміз. Тік бұрыш 3 – ке және 4 – ке тең қабырғалар арасында болады. Қабырғалардың ұштарының арақашықтығы 5 – ке тең болады.
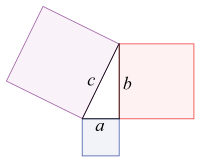
Тік бұрышты үшбұрыштың гипотенузасына салынған квадраттың ауданы катеттеріне салынған квадраттардың аудандарының қосындысына тең…
Бұл Пифагор теоремасы деп аталатын ежелден белгілі геометриялық теорема. Гректің ұлы математигі , әрі философы Пифагор Самосский осыдан 2,5 мың жыл бұрын өмір сүрген. Пифагор Шығыс елдеріне, Египетке және Вавилонға көп саяхат жасаған.Оңтүстік Италияның грек колонияларының бірінде ежелгі Грецияның ғылыми және саяси өмірінде үлкен роль атқарған белгілі «Пифагор мектебінің» негізін салған. Бұл белгілі геометриялық теореманың дәлелдеуін Пифагор практикада қолдана білген.
Бірақ, бұл теореманы Пифагорға дейін 1500 жыл бұрын ежелгі египеттіктер қабырғалары 3,4 және 5 тең болатын үшбұрыш тікбұрышты болатынын білген және бұл қасиетті жер учаскелерін, құрылыс тұрғызу үшін қолданған. Сонымен қатар мың жылдықтар бұрын Египеттегі, Вавилондағы, Қытайдағы үлкен храмдар салу үшін де қолданған. Пифагордан 600 жыл бұрын қытайдың математика-астрономиялық «Чжоу-би» шығармасында тікбұрышты үшбұрышқа қатысты басқа да теоремалар арасында Пифагор теоремасы да бар. Бұдан да ертерек теорема үндістерге де белгілі болған.
Теореманың қарапайым дәлелдеуі
Тік бұрышты үшбұрыштың гипотенузасына салынған квадрат катеттеріне салынған квадраттардың қосындысымен тең шамалы. Теореманың қарапайым дәлелдеуі тең бүйірлі үшбұрыш жағдайында қарастырылады. Tеореманың өзі де осыдан басталған.
Теореманың дұрыстығына көз жеткізу үшін тең бүйірлі тікбұрышты үшбұрыштар мозаикасына қарау жеткілікті. Мысалы, ΔABC үшін : АС гипотенузасына салынған квадрат 4 үшбұрыштан құралған, ал катеттерге салынған квадраттардың әрқайсысы екі үшбұрыштан тұрады. Теорема дәлелденді.
Фигуралардың тең шамалылығын пайдала отырып дәлелдеу
Берілген тікбұрышты үшбұрыштың гипотенузасына салынған квадрат катеттерге салынған квадраттар құрастырылған фигуралардан тұратынын дәлелдеуді қарастыруға болады. 2 суретте екі тең квадраттар бейнеленген. Әрбір квадраттың қабырғаларының ұзындығы а + b-ға тең. Квадраттардың әрбіреуі квадраттар мен тікбұрышты үшбұрыштардан тұратын бөліктерге бөлінген.Егер квадрат ауданынан катеттері а және b-ға тең тік бұрышты үшбұрыштың 4 еселенген ауданын алып тастасақ, онда тең шамалы аудандар қалады, яғни c2 = a2 + b2 . Бұл дәлелдеуді ұсынған ежелгі үндістер дәлелдеуді жазбаған, тек сызбаны «қара!» деген сөзбен түсіндірген.
Аддитивті дәлелдеулер
Бұл дәлелдеулер катеттерге салынған квадраттар жіктелген фигуралардан гипотенузаға салынған квадратты құрастыруға болатынына негізделген.
- Энштейн дәлелдеуі: гипотенузаға салынған квадратты 8 үшбұрыштарға бөлуге негізделген. Бұл жерде: ABC –тікбұрышы С болатын тікбұрышты үшбұрыш. C MN; CK MN; PO||MN; EF||MN.
- Пифагор теоремасын Евклидтің «Бастамалар» шығармасының ортағасырлық бағдадтық комментаторы ан-Найризия ұсынған бөлулер көмегімен дәлелдеу келтірілген. Бұл жағдайда гипотенузаға салынған квадрат 3 үшбұрышқа және 2 төртбұрышқа бөлінген.Мұнда: ABC – тікбұрышы C болатын үшбұрыш; DE = BF.
ан-Найризияның дәлелдеуінің негізінде квараттарды қос-қостан тең болатын фигураларға бөлуге де болады ( 5-сурет, бұл жерде ABC – C бұрышы тік болатын тікбұрышты үшбұрыш.).
- Квадраттарды тең бөліктерге жіктеу әдісі арқылы тағы бір дәлелдеу «қалқаншалы дөңгелек» деп аталады және 6-суретте көрсетілген. Мұнда: ABC– тікбұрышы C болатын тікбұрышты үшбұрыш; O – үлкен катетке салынған квадраттың центрі, О нүктесі арқылы өтетін пунктирлі түзулер гипотенузаға перпендикуляр немесе параллель.
Қосымша салулар арқылы дәлелдеу.
Бұл әдістің негізі тең шамалы фигуралар пайда болу үшін катеттерге салынған квадраттарға және гипотенузаға салынған квадратқа тең фигуралар салынады.
- қарапайым Пифагор фигурасы, яғни қабырғаларына квадрат салынған АВС тікбұрышты үшбұрышы бейнеленген. Бұл фигура алдыңғы тікбұрышты үшбұрышқа тең 1 және 2 үшбұрыштарымен толықтырылады.
- Пифагор фигурасы қабырғалары катеттерге салынған квадраттар қабырғаларына параллель тіктөртбұрышқа толықтырылады.Бұл тіктөртбұрыш үшбұрыштар мен тіктөртбұрыштарға бөленеді. Пайда болған тіктөртбұрыштан 1,2,3,4,5,6,7,8,9 көпбұрыштарын алып тастаймыз, сонда гипотенузаға салынған квадрат қалады. Енді осы тіктөртбұрыштан 5,6,7 және штрихталған тіктөртбұрыштарды алып тастасақ, катеттерге салынған квадрат пайда болады. Енді бірінші жағдайда алып тасталған фигуралар мен екінші жағдайда алып тасталған фигуралар тең шамалы екендігін дәлелдейміз.
-
Гофман (1821 ж.) дәлелдеуі. Мұнда : ABC -тік бұрышы С болатын тікбұрышты үшбұрыш; BF кесіндісі CB кесіндісіне перпендикуляр және тең, BE кесіндісі AB кесіндісіне перпендикуляр және тең, AD кесіндісі AC -ға перпендикуляр және тең; F, C, D нүктелері бір түзудің бойында жатады; ADFB және ACBE төртбұрыштары теңшамалы, өйткені ABF=ECB; ADF және ACE үшбұрыштары тең шамалы; енді екі тең шамалы төртбұрыштан да екеуіне ортақ АВС үшбұрышын алып тастаймыз, сонда мына теңдікті аламыз:
Алгебралық әдіспен дәлелдеу.
- Ұлы үнді математигі Бхаскаридің дәлелдеуі.
- ABC – тік бұрышы С болатын тікбұрышты үшбұрыш, CM AB, b1 – гипотенузаға түсірілген b катетінің проекциясы, a1 – гипотенузаға түсірілген а катетінің проекциясы, h – үшбұрыштың гипотенузаға түсірілген биіктігі.
ABC үшбұрышы мен ACM үшбұрышының ұқсастығынан
b2 = cb1; (1)
ABC , BCM үшбұрыштарының ұқсастығынан
a2 = ca1. (2) шығады. (1) және (2) теңдіктерін мүшелеп қоссақ, a2 + b2 = cb1 + ca1 = c(b1 + a1) = c2 теңдігін аламыз.
- Мёльманн дәлелдеуі -1 әдісі.
Тікбұрышты үшбұрыштың ауданы -ға немесе -ға тең, мұнда p – үшбұрыштың жарты периметрі, r – үшбұрышқа іштей сызылған шеңбердің радиусы Осыдан:
c2=a2+b2. теңдігі шығады.
Мёльманн дәлелдеуі-2 әдісі Тікбұрышты үшбұрыштың ауданы :S=½*a*b немесе S=½(p*r) тең (кез-келген үшбұрыш үшін);
p — үшбұрыштың жарты периметрі ; r – Іштей сызылған шеңбердің радиусы.
r = ½*(a + b — c) – кез-келген үшбұрышқа іштей сызылған шеңбер радиусы.
½*a*b = ½*p*r = ½(a + b + c)*½(a + b — c);
a*b = (a + b + c)*½(a + b — c);
a + b=x;
a*b = ½(x + c)*(x — c)*a*b = ½(x2-c2)
a*b = ½(a2 + 2*a*b + b2 — c2) a2 + b2 — c2 = 0, сондықтан a2 + b2 = c2
Туменбаева Жазира Куандыковна





